今さらと思われるかもしれませんが...
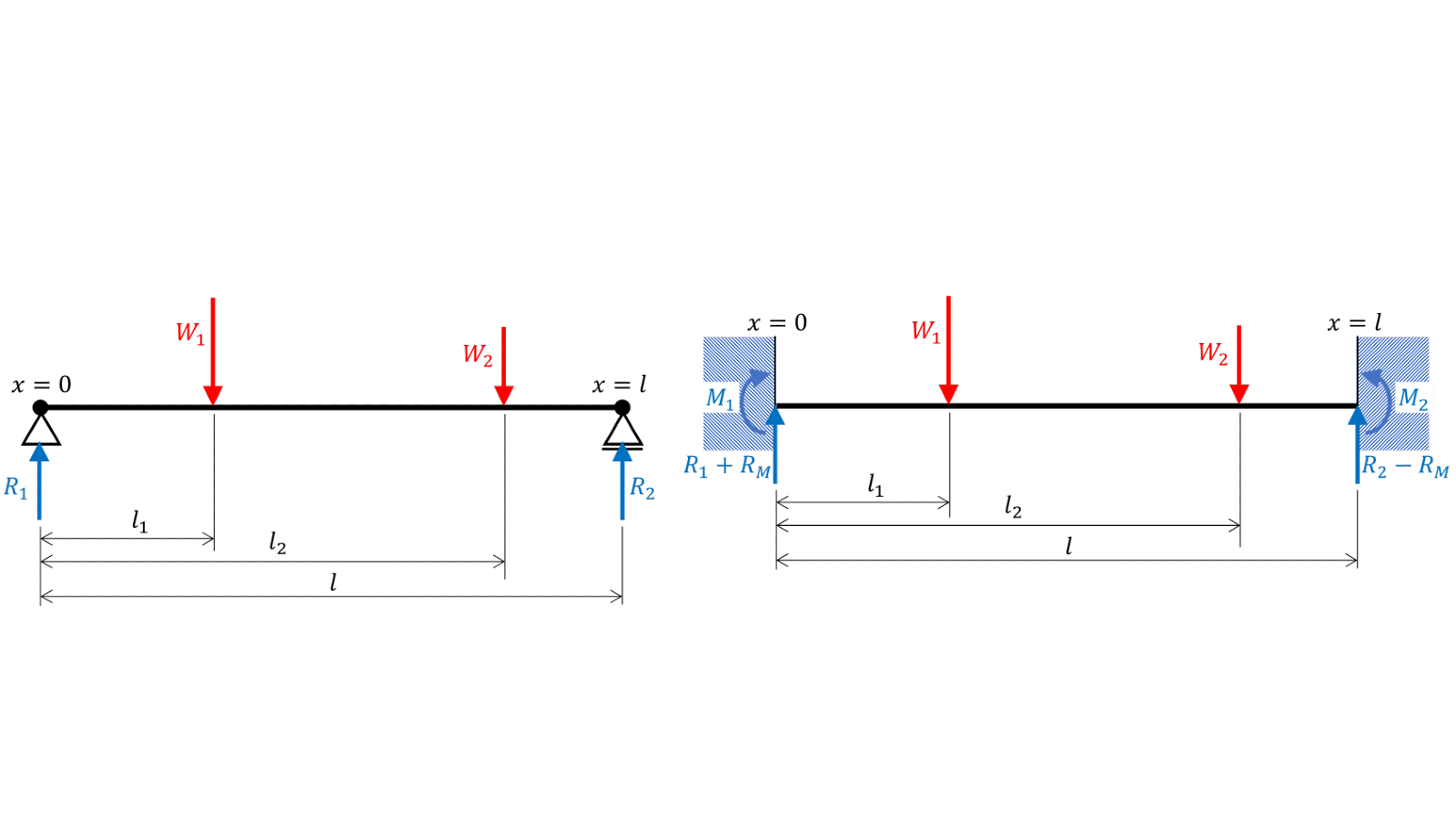
両端固定の集中2荷重による梁の撓み曲線の方程式は,書籍やインターネットなどどこを捜しても見つかりませんでした。
しかたがないので自分で作りました。他でも何かの役に立つかもしれないと思い,公開しました。
【免責事項】
検証は十分実施していますが,計算結果の扱いは自己責任でお願いします。
提供内容の使用結果に関しては,直接間接を問わず当サイトは一切の責任を負いません。
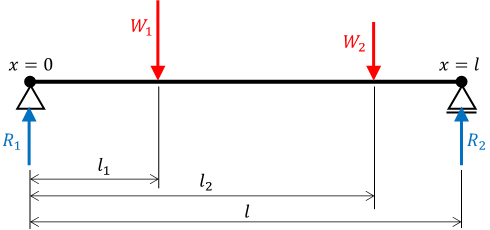
\[ \begin{array}{l} \displaystyle{R_1=W_1\,\frac{l-l_1}{l}+W_2\,\frac{l-l_2}{l}}\\ R_2=W_1+W_2-R_1 \end{array} \]
\[ F=\left\{ \begin{array}{lll} F_1 & =R_1 &\quad 0 \le x\lt l_1\\ F_2 & =R_1-W_1 &\quad l_1\lt x\lt l_2\\ F_3 & =R_1-W_1-W_2 &\quad l_2\lt x\le l \end{array}\right. \]
\[ M=\left\{ \begin{array}{ll} F_1\, x &\quad 0 \le x\le l_1\\ F_2\, x+W_1\, l_1 &\quad l_1\le x\le l_2\\ F_3\, x+W_1\, l_1+W_2\, l_2 &\quad l_2\le x\le l \end{array}\right. \]
\[ v=\left\{ \begin{array}{ll} \displaystyle{-\frac{1}{EI}\left(\frac{F_1}{6}x^3+C_1x\right)} &\quad 0\leq x\leq l_1\\ \displaystyle{-\frac{1}{EI}\left(\frac{F_2}{6}x^3+\frac{W_1\, l_1}{2}x^2+C_2\, x+C_3\right)} &\quad l_1\le x\le l_2\\ \displaystyle{-\frac{1}{EI}\left(\frac{F_3}{6}x^3+\frac{W_1\, l_1+W_2\, l_2}{2}x^2+C_4\, x+C_5\right)} &\quad l_2\le x\leq l \end{array}\right. \]
\[ \begin{array}{l} \displaystyle{C_1=\frac{W_1}{2}{l_1}^2+C_2}\\ \displaystyle{C_2=\frac{W_2}{2}{l_2}^2+C_4}\\ \displaystyle{C_3=\frac{W_1}{6}{l_1}^3}\\ \displaystyle{C_4=-\frac{W_1\,l_1\,(2\,l\,^2+{l_1}^2\,)+W_2\,l_2\,(2\, l\,^2+{l_2}^2\,)}{6\, l}}\\ \displaystyle{C_5=\frac{W_1\,{l_1}^3+W_2\,{l_2}^3}{6}} \end{array} \]
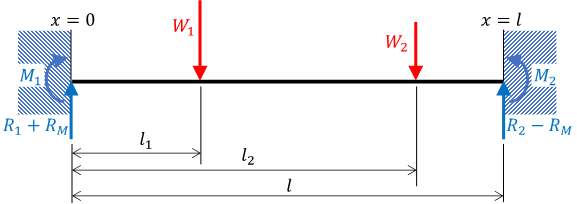
\[ \begin{array}{l} \displaystyle{R_1=W_1\,\frac{l-l_1}{l}+W_2\,\frac{l-l_2}{l}}\\ R_2=W_1+W_2-R_1\\ \displaystyle{R_M=-\frac{M_1-M_2}{l}} \end{array} \]
\[ F=\left\{ \begin{array}{lll} F_1 & =R_1+R_M &\quad 0 \le x\lt l_1\\ F_2 & =R_1-W_1+R_M &\quad l_1\lt x\lt l_2\\ F_3 & =R_1-W_1-W_2+R_M &\quad l_2\lt x\le l \end{array}\right. \] \[ R_M=\frac{W_1\,l_1\,(\,l\,^2-3\,l_1\,l+2\,{l_1}^2\,)+W_2\,l_2\,(\,l\,^2-3\,l_2\,l+2\,{l_2}^2\,)}{l\,^3} \]
\[ M=\left\{ \begin{array}{ll} F_1\, x+M_1 &\quad 0 \le x\le l_1\\ F_2\, x+W_1\, l_1+M_1 &\quad l_1\le x\le l_2\\ F_3\, x+W_1\, l_1+W_2\, l_2+M_1 &\quad l_2\le x\le l \end{array}\right. \] \[ \begin{array}{l} \displaystyle{M_1=-\frac{W_1\,l_1\,(\,l-l_1)^2+W_2\,l_2\,(\,l-l_2)^2}{l\,^2}}\\ M_2=R_M\,l+M_1\\ \displaystyle{\quad\;\;\,=-\frac{W_1\,{l_1}^2\,(\,l-l_1)+W_2\,{l_2}^2\,(\,l-l_2)}{l\,^2}} \end{array} \]
\[ v=\left\{ \begin{array}{ll} \displaystyle{-\frac{1}{EI}\left(\frac{F_1}{6}x^3+M_1x^2\right)} &\quad 0\leq x\leq l_1\\ \displaystyle{-\frac{1}{EI}\left(\frac{F_2}{6}x^3+\frac{W_1\, l_1+M_1}{2}x^2+C_2\, x+C_3\right)} &\quad l_1\le x\le l_2\\ \displaystyle{-\frac{1}{EI}\left(\frac{F_3}{6}x^3+\frac{W_1\, l_1+W_2\, l_2+M_1}{2}x^2+C_4\, x+C_5\right)} &\quad l_2\le x\leq l \end{array}\right. \]
\[ \begin{array}{l} \displaystyle{C_2=-\frac{W_1}{2}{l_1}^2}\\ \displaystyle{C_3=\frac{W_1}{6}{l_1}^3}\\ \displaystyle{C_4=-\frac{W_1\, {l_1}^2+W_2\, {l_2}^2}{2}}\\ \displaystyle{C_5=\frac{W_1\, {l_1}^3+W_2\, {l_2}^3}{6}} \end{array} \]
今回紹介した「集中2荷重による撓み曲線(両端支持と両端固定)」の解説書は こちら です。
下のサンプルを計算した Excel を提供しています。
こちら からダウンロードできます。
工事中
片端固定と片持ちを検討する予定です